Our professional faculty has curated these NCERT Solutions to aid students in their term-by-term exam preparation. Students looking for NCERT Solutions for Class 10 Maths can download complete chapter-by-chapter to help them solve questions more effectively.
All the solutions of the NCERT books are without a doubt the best study material available for the students. These CBSE NCERT solutions for Class 10 Maths will also help the students in developing a more in-depth grasp of subjects presented in the textbook. Practicing the questions from the textbook will assist pupils in assessing their degree of preparation and subject comprehension. This solved exercise has very helpful for your exam.
NCERT Solutions Class 10 Maths All Chapters:
Practice Comprehensively with Oswaal360 CBSE Online Courses for Class 10 Board Exams 2025
Practice Now with Free Oswaal360 Online Mock Test for CBSE Class 10 Board Exams 2025
Are You a Teacher? Apply for FREE CBSE Class 10 Specimen Sample Books For Teachers from our end.
 In our website we upload all the solution of NCERT chapter. The expert written in a very clear and logical manner while all textbook's objectives questions. The NCERT Solutions is used as an important part of your math subject.
In our website we upload all the solution of NCERT chapter. The expert written in a very clear and logical manner while all textbook's objectives questions. The NCERT Solutions is used as an important part of your math subject.
The NCERT Solutions for Class 10 Maths list contains all of the chapter-wise solutions to the NCERT Book for Class 10 Maths problems, given clearly and transparently while preserving the textbook's purpose. The NCERT Solutions for 10th Class can be used as extra references and study tools by students. Practicing NCERT textbook exercise answers would undoubtedly aid students' test preparation.
These assist students in comprehending or solving the sorts of problems that a paper setter asks in the board examinations for CBSE Class 10 Maths. Furthermore, offering solutions to all areas relating to circles assists students in effectively preparing for the board examinations.
The subject matter experts make sure that the errors in the NCERT textbooks are resolved according to the NCERT rules and syllabus.
The solutions to the NCERT-based questions for all the chapters of Class 10 Maths are accessible at Oswaal CBSE Class 10 Maths. These solutions will assist students in acing their board examinations by preparing for the examinations ahead of time. Students may clarify all of their conceptual questions or doubts with the assistance of the notes provided in Maths NCERT Solutions for Class 10 of all the chapters. Experts have created these NCERT Solutions based on the most recent update to the CBSE Syllabus to help students in Class 10 prepare well for their term-wise examinations.
The NCERT Solutions Chapter 1 Real Number for Class 10 Maths:
Students in grade 10 will investigate real and irrational numbers in Chapter 1. The chapter begins with Euclid's Division Lemma, which asserts that "given two positive numbers a and b, there are two distinct integers q and r fulfilling
a= bq + r, 0 ≤ r < b."
Based on this lemma, Euclid's Division technique is used to determine the HCF of two positive numbers. The Fundamental Theorem of Arithmetic, which is utilized to compute the LCM and HCF of two positive integers, is then defined. The idea of an irrational number, a rational number, and the decimal expansion of rational numbers are then described using a theorem.
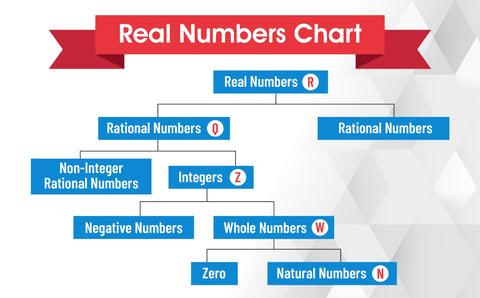
Real Numbers:
A quantity that may be stated as a limitless decimal expansion in mathematics is a real number. Unlike natural numbers 1, 2, 3... derived from counting, real numbers are utilized to measure constantly altering quantities such as size and time. Real numbers are represented by R.
Real numbers are classified into two types, i.e., rational and irrational numbers.
|
CBSE Sample Papers Class 10 | For Upcoming Board Exams |
|
|
CBSE Question Banks Class 10 | For 2024-25 Board Exams |
|
|
CBSE Previous Year Question Papers Class 10 | For 2025 Board Exams |
|
|
NCERT Exemplar Class 10 | For 2025 Board Exams |
|
|
CBSE Class 10 RMT Flashcards | For Upcoming Board Exams |
|
|
CBSE Class 10 LMP |
|
|
CBSE One for All Class 10 | For 2025 Board Exams |
|
|
CBSE Class 10 Syllabus | For 2025 Board Exams |
|
|
NCERT Books Class 10 | For 2025 Board Exams |
|
|
Free CBSE ICSE Specimen Sample Books for Teachers |
Rational number:
A number may be expressed as the quotient p/q of two integers, with q ≠ 0. In addition to fractions, the set of rational numbers includes all integers. Each can be described as a quotient with the integer as the numerator and one as the denominator. Rational numbers are represented by Q.
Rational numbers are divided into two subparts, i.e., non-integer rational numbers and rational integer numbers.
Integer rational numbers are those rational numbers made up of integers, whereas non-integer rational numbers do not contain integers.
This class of rational numbers, i.e., integers, is further classified into two groups, i.e., negative and whole numbers. Thus, whole numbers are the numbers that are the combination of natural numbers along with 0.
Irrational numbers
Those types of real numbers, which are not rational, are referred to as irrational numbers. Irrational numbers, in other words, cannot be stated as the ratio of two integers. When the length ratio of two-line segments is an irrational number, the line segments are said to be incommensurable, which means that they have no "measure" in common. That is, no length ("the measure"), no matter how small, can be employed to convey the lengths of both given segments as integer multiples of itself.
Chapter 1 Real Numbers:
The Fundamental Theorem of Arithmetic claims made after analysing previous work and showing and inspiring with examples. The representation of rational numbers in decimal terms in terms of terminating/non-terminating recurring decimals.
Important Steps to Take
To get the HCF of two positive numbers, say c and d, with c > d, apply the following steps:
Step 1: Apply the division lemma of Euclid to c and d. So, we look for whole numbers, q and r, such that c = dq + r, 0≤ r< d.
Step 2: If r = 0, the HCF of c and d equals d. We apply the division lemma to d and r if r = 0.
Step 3: Repeat the process until the remaining equals zero. At this point, the divisor will be the desired HCF. This approach works because HCF (c, d) = HCF (d, r), where HCF (c, d) represents the HCF of c and d, respectively.
NCERT Solutions for 10th Grade Maths Chapter 1 Exercises:
|
Exercise 1.1 NCERT Solutions of the REAL NUMBERS chapter of Class 10 |
|
Exercise 1.2 NCERT Solutions of the REAL NUMBERS chapter of Class 10 |
|
Exercise 1.3 NCERT Solutions of the REAL NUMBERS chapter of Class 10 |
|
Exercise 1.4 NCERT Solutions of the REAL NUMBERS chapter of Class 10 |
Also available at CBSE Class 10 Books contains the following materials for NCERT Class 10 Chapter 1 Real Numbers:
Chapter 2 Polynomials –NCERT Solutions for Class 10 Maths:
The chapter Polynomials opens with a definition of the degree of a polynomial, a linear polynomial, a quadratic polynomial, and a cubic polynomial. This chapter has four exercises, one of which is optional. Exercise 2.1 covers questions about determining the number of zeroes in a graph. It necessitates a grasp of the Polynomial's Zeroes Geometrical Meaning. Exercise 2.2 is based on the Zeroes and Coefficients of a Polynomial's relationship. In some of the problems, students must discover the zeros of a quadratic polynomial and the quadratic polynomial. The idea of the division algorithm is described in Exercise 2.3, and students will find questions connected to it. The optional Exercise, 2.4, contains questions from all of Chapter 2's topics.
Polynomials
Polynomials are sums of k⋅xⁿ terms, where k can be any number and n can be any positive integer. 3x+2x-5, for example, is a polynomial. A polynomial is an expression in mathematics that consists of indeterminates (also known as variables) and coefficients and includes only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables. x2-4x + 7 is an example of a polynomial with a single indeterminate x. In three variables, consider x3 + 2xyz + 2yz + 1. Polynomials may be found in many fields of mathematics and science.
Zeros of Polynomial
A polynomial's zeros are all the x-values that make the polynomial equal zero. They are fascinating to us for various reasons, one of which is that they reveal the x-intercepts of the polynomial graph. These are closely related to the polynomial factors.
Topics that are covered in Chapter 2: Polynomials for Class 10 Maths
The topics of the relationship between zeroes, coefficients of quadratic polynomials, and zeroes of a polynomial are covered in Chapter 2, i.e., Polynomials for Class 10 Maths.
Steps to Take
We begin by arranging the dividend and divisor words in decreasing order of their degrees. Remember that putting the terms in this sequence is referred to as "writing polynomials in standard form."
Step 1: To get the first term of the quotient, divide the dividend's highest degree term by the divisor's highest degree term. Then proceed with the dividing procedure.
Step 2: To get the second term of the quotient, divide the highest degree term of the new dividend by the divisor's highest degree term. Carry out the dividing procedure once again.
Step 3: The remainder degree is now smaller than the divisor's degree. As a result, we cannot continue to divide.
We can see that Dividend = Divisor × Quotient + Remainder once more. We're using an approach similar to Euclid's division algorithm, which you learned about in Chapter 1.
There are two polynomials p(x) and g(x) with g(x) ≠ 0, we may evaluate polynomials h(x) and m(x) such that p(x) = g(x) × h(x) + m(x), where m(x) = 0 or degree of m(x) < degree of g (x).
This is known as the Polynomial Division Algorithm.
NCERT Solutions for Class 10 Maths Chapter 2 Exercises:
|
Exercise 2.1 NCERT Solutions of the POLYNOMIALS chapter of Class 10 |
|
Exercise 2.2 NCERT Solutions of the POLYNOMIALS chapter of Class 10 |
|
Exercise 2.3 NCERT Solutions of the POLYNOMIALS chapter of Class 10 |
|
Exercise 2.4 NCERT Solutions of the POLYNOMIALS chapter of Class 10 |
Our CBSE Class 10 books also has the following resources for NCERT Class 10 Chapter 2 Polynomials:
Class 10 Maths NCERT Solutions of Chapter 3: Pair of Linear Equations in Two Variables
The concept or idea of a "Pair of Linear Equations in Two Variables" is explained in this chapter. This chapter has seven problems, each of which describes a different approach to solving the pair of linear equations. Exercise 3.1 describes how to algebraically and visually depict a scenario. Exercise 3.2 illustrates how to solve the pair of linear equations using the graphical method. The Algebraic, Elimination, Cross-Multiplication Method, and Substitution Methods are described in Exercises 3.3, 3.4, 3.5, and 3.6. Exercise 3.7 is an optional exercise with a variety of questions. Students must practice these activities to grasp the process of solving linear equations.
Linear equation in two variables
It is defined as an equation which is in the form dx+ny+l, where d, n, and l are absolute values, and d and n are not equal to zero. It is known as the linear equation in two variables.
Topics that are covered in Chapter 3: Pair of Linear Equations in two variables for Class 10 Maths:
Several solutions have algebraic conditions: a pair of two-variable linear equations, their graphical solutions, and their consistency and inconsistency. A pair of linear equations' algebraic solutions in two variables using substitution and elimination. Simple situational and equation problems can be reduced to linear equations.
Formulas of Importance
The general form of the pair of linear equations in two variables, i.e., x and y are f1 x + g1 y + h1 = 0 and f2 x + g2 y + h2 = 0, where f1, g1, h1, f2, g2, h2 are all real integers and f12 + g12 ≠ 0, f22 + g22 ≠ 0
Class 10 Maths Chapter 3 NCERT Solutions Exercises
|
Exercise 3.1 NCERT Solutions of the Pair of Linear Equations in Two Variables Chapter of Class 10 |
|
Exercise 3.2 NCERT Solutions of the Pair of Linear Equations in Two Variables chapter of Class 10 |
|
Exercise 3.3 NCERT Solutions of the Pair of Linear Equations in Two Variables chapter of Class 10 |
|
Exercise 3.4 NCERT Solutions of the Pair of Linear Equations in Two Variables chapter of Class 10 |
|
Exercise 3.5 NCERT Solutions of the Pair of Linear Equations in Two Variables chapter of Class 10 |
|
Exercise 3.6 NCERT Solutions of the Pair of Linear Equations in Two Variables chapter of Class 10 |
|
Exercise 3.7 NCERT Solutions of the Pair of Linear Equations in Two Variables chapter of Class 10 |
Our CBSE Class 10 books also has the following resources for NCERT Class 10 Chapter 3 Pair of Linear Equations in Two Variables:
NCERT Solutions for Grade 10 Maths Chapter 4 Quadratic Equations:
Students will learn the traditional manner of formulating a Quadratic Equation in this chapter. The chapter then explains how to solve a quadratic problem using the factorization approach and complete the square method. The chapter concludes with determining the nature of roots, which asserts that a quadratic equation ax² + bx + c = 0 has two separate real roots if b² – 4ac > 0 and two equal roots if b² – 4ac = 0.
If b² – 4ac < 0, there are no genuine roots.
Chapter 4 Quadratic Equations of Class 10 Maths:
The standard form of a quadratic equation is ax2 + bx + c = 0 (a ≠ 0). Factorization and the quadratic formula solve quadratic equations (only real roots). The relationship between the discriminant and the nature of the roots. Situational questions based on quadratic equations that are relevant to everyday activities (problems on equations reducible to quadratic equations are excluded)
Formula:
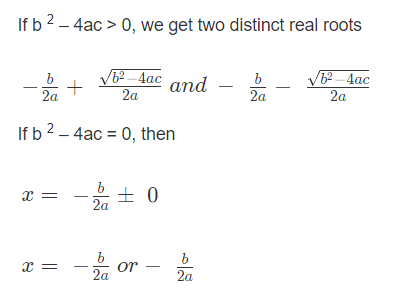
As a result, the roots of ax2 + bx + c = 0 are both -b/2a.
As a result, in this example, the quadratic equation ax2 + bx + c = 0 has two equal real roots.
There is no real integer whose square is b2 – 4ac if b2 – 4ac = 0. As a result, there are no true roots for the given quadratic equation in this example.
Because b2 – 4ac decides whether or not the quadratic equation ax2 + bx + c = 0 has real roots, it is the discriminant of this quadratic equation.
As a result, the quadratic equation ax2 + bx + c = 0 has
NCERT Solutions for Grade 10 Maths Chapter 4 Exercises
|
Exercise 4.1 NCERT Solutions of the Quadratic Equations Chapter of Class 10 |
|
Exercise 4.2 NCERT Solutions of the Quadratic Equations chapter of Class 10 |
|
Exercise 4.3 NCERT Solutions of the Quadratic Equations chapter of Class 10 |
|
Exercise 4.4 NCERT Solutions of the Quadratic Equations chapter of Class 10 |
Also available in Our CBSE Class 10 books with the following materials for NCERT Class 10 Chapter 4 Quadratic Equations:
Chapter 5 Arithmetic Progressions NCERT Solutions for Class 10 Maths
This chapter introduces students to Arithmetic Progression, abbreviated as AP. There are four exercises in this chapter. Students will discover questions in Exercise 5.1 about describing a scenario in the form of AP, evaluating the first term and difference of an AP, and determining if a series is AP or not. Exercise 5.2 offers questions about calculating the nth term of an AP using the following formula:
an = a + (n-1) d
The next Exercise, 5.3, offers questions on calculating the sum of the first n terms of an AP.
The last Exercise contains AP-based higher-level problems to help students improve their analytical and problem-solving abilities.
Class 10 Maths Chapter 5 Arithmetic Progressions:
Why do you want to learn about Arithmetic Progression? The nth term and the sum of the first n terms of A.P. are deduced and used to solve difficulties in everyday life.
(Applications based on an A.P.'s sum to n words are not permitted.)
Formulas of Importance
If the terms of AP are a1, a2, a3, a4, a5, a6... and d is the common difference between each term, then the sequence is an a+d, a+2d, a+3d, a+4d, a+5d,...., nth term..., where an is the first term. The nth term for mathematical progression is now;
a + (n-1) d = nth term
Arithmetic Progression's first n terms' sum;
Sn = n/2 [2a + (n-1) d]
NCERT Solutions for Class 10 Maths Chapter 5 Exercises:
|
Exercise 5.1 NCERT Solutions of the Arithmetic Progressions Chapter of Class 10 |
|
Exercise 5.2 NCERT Solutions of the Arithmetic Progressions chapter of Class 10 |
|
Exercise 5.3 NCERT Solutions of the Arithmetic Progressions chapter of Class 10 |
|
Exercise 5.4 NCERT Solutions of the Arithmetic Progressions chapter of Class 10 |
Our CBSE Class 10 books also has the following materials for NCERT Class 10 Chapter 5 Arithmetic Progressions:
Chapter 6 Triangles : NCERT Solutions for Class 10 Maths
Students in 10th Grade CBSE Maths will study figures with the same shape but not necessarily the same size in Chapter 6. Triangles begin with the notion of a comparable and harmonious form. It goes on to describe the criteria for the similarity of two triangles as well as theorems about triangle similarity. Following that, the areas of identical triangles were defined using a theorem. The Pythagoras Theorem and its converse are discussed at the conclusion of this chapter.
Class 10 Maths Chapter 6 Triangles: Definitions, examples, and counter examples of related triangles
Theorems of Importance
Theorem 6.1: At one side of a triangle, a parallel line is drawn, which intersects the other two sides in distinct spots; the remaining two sides are split in the same ratio.
Theorem 6.2: A line is parallel to the third side if it divides any of the two sides of a triangle in the same ratio.
Theorem 6.3: If the corresponding angles in two triangles are identical, their corresponding sides are in the same ratio (or percentage), and the two triangles are comparable.
Theorem 6.4: If the sides of one triangle in two triangles are proportional to (i.e., in the same ratio as) the sides of the other triangle, then their corresponding angles are equal, and thus the two triangles are comparable.
Theorem 6.5: If one angle of one triangle equals one angle of another triangle, and the sides containing these angles are proportionate, the two triangles are identical.
Theorem 6.6: The ratio of the two comparable triangle areas is equal to the square of the ratio of their corresponding sides, according to Theorem 6.6.
Theorem 6.7 states that if a perpendicular is drawn from the vertex of a right triangle's right angle to the hypotenuse, triangles on both sides of the perpendicular are comparable to the complete triangle.
Theorem 6.8: The square of the hypotenuse of a right triangle is equal to the sum of the other two sides square.
Theorem 6.9: When the square of one side of a triangle equals the summation of the squares of the other two sides, the angle opposite the first side is right.
NCERT Solutions for Class 10 Maths Chapter 6 Exercises
|
Exercise 6.1 NCERT Solutions of the Triangles Chapter of Class 10 |
|
Exercise 6.2 NCERT Solutions of the Triangles chapter of Class 10 |
|
Exercise 6.3 NCERT Solutions of the Triangles chapter of Class 10 |
|
Exercise 6.4 NCERT Solutions of the Triangles chapter of Class 10 |
|
Exercise 6.5 NCERT Solutions of the Triangles chapter of Class 10 |
|
Exercise 6.6 NCERT Solutions of the Triangles chapter of Class 10 |
Our CBSE Class 10 books also has the following materials for NCERT Class 10 Chapter 6 Triangles:
Chapter 7 Coordinate Geometry: NCERT Solutions for Class 10 Maths
Students will learn how to calculate or evaluate the distance between two locations whose coordinates are supplied and the area of a triangle formed by three specified points in this chapter. Students will also learn how to identify the coordinates of the point that splits a line segment connecting two specified points in a specific ratio. Students will study the Distance Formula, Section Formula, and Area of a Triangle in this chapter of Coordinate Geometry.
Coordinate Geometry
The geometrical study by using coordinate points is known as coordinate geometry (or analytic geometry). It is possible to estimate the distance between two points, divide lines in an m:n ratio, identify the midpoint of a line, calculate the area of a triangle in the Cartesian plane, and so on using coordinate geometry.
Class 10 Maths Chapter 7 Coordinate Geometry:
Lines (In two dimensions)
Concepts of coordinate geometry and graphs of linear equations are reviewed.
Distance calculation formula
The formula for Sections (internal division)
Important formula
Distance Formula
![]()

NCERT Solutions for Class 10 Maths Chapter 7 Exercises
|
Exercise 7.1 NCERT Solutions of the Coordinate Geometry Chapter of Class 10 |
|
Exercise 7.2 NCERT Solutions of the Coordinate Geometry chapter of Class 10 |
|
Exercise 7.3 NCERT Solutions of the Coordinate Geometry chapter of Class 10 |
|
Exercise 7.4 NCERT Solutions of the Coordinate Geometry chapter of Class 10 |
Our CBSE Class 10 Books also has the following materials for NCERT Class 10 Chapter 7 Coordinate Geometry:
Chapter 8 Introduction to Trigonometry: NCERT Solutions for Class 10 Maths
Trigonometry will be introduced to pupils in this chapter. They will investigate trigonometric ratios of angles, ratios of a right triangle to its sharp angles. The chapter also defines trigonometric ratios for angles ranging from 00 to 900. Students will also understand how to compute trigonometric ratios for specific angles and create trigonometric identities employing these ratios.
Chapter 8 of Class 10 Maths: Trigonometry Overview
Trigonometric ratios of a right-angled triangle's acute angle Evidence of their existence (well defined). Trigonometric ratio values of 300, 450, and 600. Relationships among the ratios
IDENTITIES TRIGONOMETRIC
Application and proof of the identity sin2 A + cos2 A = 1. Only simple identities will be provided.
Important formulas
Trigonometry Maths Formulas for Class 10 address three key functions for a right-angle triangle: Sine, Cosine, and Tangent. Assume that a right-angled triangle ABC is right-angled at point B and has ∠θ.
Trigonometry Table
|
Angle |
0° |
30° |
45° |
60° |
90° |
|
Sin θ |
0 |
1/2 |
1/√2 |
√3/2 |
1 |
|
Cos θ |
1 |
√3/2 |
1/√2 |
1/2 |
0 |
|
Tan θ |
0 |
1/√3 |
1 |
√3 |
Undefined |
|
Cot θ |
Undefined1 |
√3 |
1 |
1/√3 |
0 |
|
Sec θ |
1 |
2/√3 |
√2 |
2 |
Undefined |
|
Cosec θ |
Undefined |
2 |
√2 |
2/√3 |
1 |
Trigonometric Ratios of Complementary Angles
NCERT Solutions pdf for Class 10 Maths Chapter 8 Exercises
|
Exercise 8.1 NCERT Solutions of the Trigonometry Chapter of Class 10 |
|
Exercise 8.2 NCERT Solutions of the Trigonometry chapter of Class 10 |
|
Exercise 8.3 NCERT Solutions of the Trigonometry chapter of Class 10 |
|
Exercise 8.4 NCERT Solutions of the Trigonometry chapter of Class 10 |
Our CBSE Class 10 books also has the following materials for NCERT Class 10 Chapter 8 Trigonometry:
NCERT Solutions for Class 10 Maths Chapter 9 Trigonometry Applications
This chapter builds on the previous one by teaching students about trigonometry applications. It is used in geography, navigation, map production, and calculating an island's location in reference to longitudes and latitudes. Students will learn how to utilize trigonometry to find the heights and distances of various objects without having to measure them. They will learn about line of sight, angle of elevation, and angle of depression.
Chapter 9 of Class 10 Maths covers the following topics: Some Trigonometry Applications
HEIGHTS AND DISTANCES-Angle of Elevation and Angle of Depression
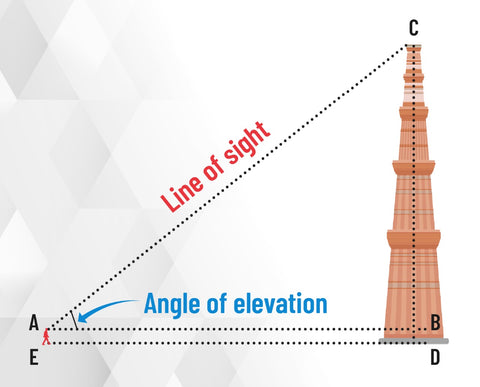
Simple height and distance issues. A problem should have no more than two right triangles. Elevation/depression angles should not exceed 30 degrees, 45 degrees, and 60 degrees.
Important Notes –
You would need to be aware of the following:
Assuming the three requirements mentioned above are met, how can we calculate the minar's height?
CD = CB + BD in the diagram. In this case, BD = AE, which is the student's height.
To calculate BC, we shall utilize trigonometric ratios of BAC or A.
The side BC in ABC is the opposite side in regard to the known A because these ratios include AB and BC, our search narrows to tan A or cot A.
As a result, tan A = BC/AB or cot A = AB/BC, which, when solved, gives us BC.
The height of the minar may be calculated by adding AE to BC.
NCERT Solutions pdf for Class 10 Maths Chapter 9 Exercises
|
Exercise 9.1 NCERT Solutions of the Some Applications of Trigonometry Chapter of Class 10 |
With our CBSE Class 10 books, you may also find the following materials for NCERT Class 10 Chapter 9 Some Applications of Trigonometry:
Chapter 10 Circles –NCERT Solutions for Class 10 Maths
Students have previously learned about a circle and different circle-related terminology such as a chord, segment, arc, etc. Students will investigate the many circumstances when a circle and a line are presented in a plane in this chapter. As a result, they will get thoroughly acquainted with the concepts of Tangent to a Circle and Number of Tangents from a Point on a Circle.
Class 10 Math Topics Chapter 10 Circles:
Point of contact tangent to a circle
Theorems of Importance –
Number of Tangents from a Circle Point
Case 1: There is no tangent to a circle that passes through a point located within the circle.
Case 2: There is only one Tangent to a circle that passes through a point on the circle.
Case 3: There are two tangents to a circle that intersects at a place outside the circle.
NCERT Solutions pdf for Class 10 Maths Chapter 10 Exercises
|
Exercise 10.1 NCERT Solutions of the Circles Chapter of Class 10 |
|
Exercise 10.2 NCERT Solutions of the Circles Chapter of Class 10 |
Our CBSE Class 10 books also has the following materials for NCERT Class 10 Chapter 10 Circles:
Chapter 11 Constructions: NCERT Solutions Class 10 Maths
There are two exercises in this chapter. Whatever learners learned about building in previous sessions will also be helpful. Students will learn how to split a line segment in Exercise 11.1 and create tangents to a circle in Exercise 11.2. Methods and processes for building are discussed, and some examples are provided to help students understand.
Class 10 Math Topics Chapter 11 Constructions:
Important Notes –
11.1: To split a line segment in a specific ratio.
11.2: Build a triangle identical to a given triangle using the specified scale factor.
11.3: To build the tangents to a circle from a location outside it.
NCERT Solutions pdf for Class 10 Maths Chapter 11 Exercises
|
Exercise 11.1 NCERT Solutions of the Constructions Chapter of Class 10 |
|
Exercise 11.2 NCERT Solutions of the Constructions chapter of Class 10 |
Our CBSE Class 10 books also has the following materials for NCERT Class 10 Chapter 11 Constructions:
NCERT Solutions for Class 10 Maths Chapter 12 Circle Areas
This chapter begins with the notions of circle perimeter and area. The chapter goes on to describe how to find the area of a sector and segment of a circular region using this notion. Furthermore, students will gain confidence in calculating the areas of various plane figure combinations involving circles or their portions.
Topics Covered in Class 10 Maths Chapter 12 Circle:
Motivate the area of a circle, the area of a circle's sections and segments. As mentioned earlier, area and perimeter/circumference problems are based on the plane. (When computing the area of a circle segment, issues should be limited to central angles of 60° and 90° only. Plane figures with triangles, basic quadrilaterals, and circles should be used.)
Circumference of the circle: A circle's perimeter is the linear distance travelled around the circle. The perimeter of a circle is known by a unique name, Circumference. The circumference multiplied by the diameter is given by the formula 2πr.
Area of circle: The circle area is πr2, where r is the circle's radius and π = 22/7 or 3.14 (maybe used interchangeably for problem-solving purposes). Thus, an area of the circle is nothing but is the ratio of a circle's circumference to its diameter.
A Circle's Segment
A circular segment is a section of a circle "separated" from the portion of the circle by a secant or chord.
A circle's sector
A circle sector is the portion of a circle bounded by an arc and two radii. The smaller region is referred to as the minor sector, while the larger area is the major sector.
A Sector's Angle
The angle of a sector is defined as the angle formed by the sector's two radii.
The Angle of a Sector
A sector's angle is defined as the angle created by the sector's two radii.
L= (θ/360°) × 2πr
Where θ is the sector angle and r is the circle's radius.
Students may also utilize this NCERT Exemplar to complete even the most challenging problems and prepare for examinations. However, sample papers and previous year's question papers are quite helpful in understanding the sorts of questions a paper setter asked in the examination from this chapter 12 and the marking system.
This chapter covers the Areas related to the Circles subjects listed below:
Students will learn to calculate various circle areas and combinations of plane figure areas, in Chapter 12.
Students in the tenth grade are also given online study tools, including notes, example books, NCERT answers, and question papers, to help them prepare for the board examinations.
This chapter may take some time to complete, and students must pay close attention. The NCERT Exemplar for Class 10 Maths is provided here to assist students in solving chapter concerns and obtaining proper answers to complex questions.
Important Formulas –
NCERT Solutions pdf for Class 10 Maths Chapter 12 Exercises
|
Exercise 12.1 NCERT Solutions of the Areas Related to Circles Chapter of Class 10 |
|
Exercise 12.2 NCERT Solutions of the Areas Related to Circles chapter of Class 10 |
|
Exercise 12.3 NCERT Solutions of the Areas Related to Circles chapter of Class 10 |
Exercise 12.1 includes five solved questions. Four of them are short answer type questions, and the remaining one is the MCQ type.
This exercise is primarily concerned with the perimeter and area of a circle. In this lesson, students learn how to determine the circumference and area using formulae and apply what they've learned to real-world problems. Solutions give an overview of the chapter's essential themes and assist students in becoming familiar with these concepts.
In this exercise 12.1 of Chapter 12, students are given the solutions to many questions to perform well in their first term examinations.
The solutions to the NCERT-based questions of Chapter 12 for Class 10 Maths, Areas Related to Circles, is an essential study resource for Class 10 students. These assist students in comprehending or solving the sorts of problems that a paper setter asked in the first term examinations of CBSE Class 10 Maths. Furthermore, offering solutions to all areas relating to circles assists students in effectively preparing for the board examinations.
The subject matter experts make sure that the errors in the NCERT textbooks are resolved according to the NCERT rules and syllabus.
The solutions to the Exercise 12.1 NCERT-based questions of Chapter 12 for Grade 10 Maths are accessible at our Oswaal books. These solutions will assist students in acing their first term examinations by preparing for the examinations ahead of time.
Students may clarify all of their conceptual questions or doubts with the assistance of the notes of Maths NCERT Solutions for Class 10 of this chapter which we provide. Experts have created these NCERT Solutions based on the most recent update to the CBSE syllabus for 2024-25 to help students in Class 10 prepare well for their term-wise examinations
Our CBSE Class 10 books also has the following resources for NCERT Class 10 Chapter 12 Areas Related to Circles:
Chapter 13 Surface Areas and Volumes - NCERT Solutions for Class 10 Maths
There are five exercises in Chapter 13. The first Exercise consists of questions on calculating the surface area of an object made by merging any two fundamental solids, namely a cuboid, cone, cylinder, sphere, and hemisphere. 13.2 questions in Exercise are focused on determining the volume of objects generated by joining any two of a cuboid, cone, cylinder, sphere, or hemispheres. Exercise 13.3 has questions on converting a solid from one shape to another. Exercise 13.4 involves calculating the volume, curved surface area, and total surface area of a cone's frustum.
Chapter 13 Surface Areas and Volumes in Class 10 Maths:
Important Formulas –
NCERT Solutions pdf for Class 10 Maths Chapter 13 Exercises
|
Exercise 13.1 NCERT Solutions of the Surface Areas and Volumes chapter of Class 10 |
|
Exercise 13.2 NCERT Solutions of the Surface Areas and Volumes chapter of Class 10 |
|
Exercise 13.3 NCERT Solutions of the Surface Areas and Volumes chapter of Class 10 |
|
Exercise 13.4 NCERT Solutions of the Surface Areas and Volumes chapter of Class 10 |
|
Exercise 13.5 NCERT Solutions of the Surface Areas and Volumes chapter of Class 10 |
Our CBSE Class 10 Books also has the following resources for NCERT Class 10 Chapter 13 Surface Areas and Volumes:
NCERT Solutions for Class 10 Maths Chapter 14 Statistics
Students will learn how to convert ungrouped data to grouped data and how to calculate the Mean, Mode, and Median. In addition, the notion of cumulative frequency, cumulative frequency distribution, and how to design cumulative frequency curves will be discussed.
Class 10 Maths Chapter 14 Statistics:
Grouped data mean, median, and mode (bimodal situation to be avoided). Only the Direct Method and the Assumed Mean Method are used to calculate the mean.
Important Formulas –
The mean of the grouped data can be found by 3 methods
1. Direct Method:


4. The mode of grouped data:
![]()
5. The median for a grouped data:
![]()
NCERT Solutions PDF for Class 10 Maths Chapter 14 Exercises
|
Exercise 14.1 NCERT Solutions of the Statistics chapter of Class 10 |
|
Exercise 14.2 NCERT Solutions of the Statistics chapter of Class 10 |
|
Exercise 14.3 NCERT Solutions of the Statistics chapter of Class 10 |
|
Exercise 14.4 NCERT Solutions of the Statistics chapter of Class 10 |
Our CBSE Class 10 books also has the following materials for NCERT Class 10 Chapter 14 Statistics:
Class 10 Maths NCERT Solutions Chapter 15 Probability
The final chapter is about Probability. The chapter begins with a theoretical look at probability. Following that, the chapter discusses the distinction between experimental and theoretical probability. There are several instances provided to illustrate it effectively. So, before proceeding with the practice questions, students must first complete the CBSE Maths examples.
Chapter 15 Probability NCERT Class 10 Maths: The classical definition of probability. Simple issues involve determining the likelihood of an event.
Important Formulas –
NCERT Solutions pdf for Class 10 Maths Chapter 15 Exercises
|
Exercise 15.1 NCERT Solutions of the Probability chapter of Class 10 |
|
Exercise 15.2 NCERT Solutions of the Probability chapter of Class 10 |
Our CBSE Class 10 books also has the following resources for NCERT Class 10 Chapter 15 Probability:
NCERT Solutions for Class 10 Maths PDF in English Medium and Hindi Medium (for the academic year 2024-25 are used not only by CBSE but also by UP Board, Uttarakhand Board, and all other boards that use NCERT Textbooks.
Advantages of NCERT Solutions Class 10 Math:
The Class 10 NCERT Math Solutions in PDF format provided here offer various advantages, including:
Students are urged to prepare all of the chapters covered in the solution modules, as this will help them obtain a deeper understanding of the subjects. Students must comprehend all of the processes outlined in the solutions to make good preparations.
How Can CBSE Class 10 Maths Solutions from NCERT Help with Term Exams?
Math in CBSE Class 10 is an essential topic for students. We have offered full preparatory support to students here. Class 10 is the initial criterion for each student that will be reflected in subsequent accomplishment records. CBSE consistently recommends NCERT books for term-by-term test preparation.
Exam preparation is a time-consuming procedure that necessitates a thorough comprehension of individual chapters. This technique necessitates diligent study and a systematic approach to completing the solutions. NCERT 10 Class Maths Solutions play an essential part in preparing students for competitive admission tests. NCERT books are well-known for presenting topics in an easy-to-understand format. NCERT Class 10 Mathematics Books are written most understandably and straightforwardly, allowing complicated problems to be broken down effectively.
Continue to visit to obtain complete chapter-by-chapter NCERT Solutions for Class 10 Maths PDF free download for all courses. NCERT Solutions for Class 10 Science may also be found at class 10. Students at class 10 benefit from a customized learning experience that helps them prepare for tests more successfully.
NCERT Solutions assist students in solidifying their knowledge of the mathematics concept.
Diagrams are used to answer questions, making learning more dynamic and thorough.
The language used in NCERT Solutions is simple and easy to grasp.
Students benefit from a step-by-step approach to problem-solving.
Allows learners to work through challenging problems in their own time.
NCERT Solutions for various courses and disciplines are also available for students to use. Well-experienced professors of class 10 books create these answers to offer clarity on essential ideas and problem-solving abilities.
Students can also obtain a firm grasp of critical topics by referring to additional study resources available at CBSE class 10 books.
The NCERT Solutions for Class 10 Maths are essential in shaping a kid's future since the grades that student achieves on the board test ultimately form the student's potential. The examinations for Classes 10 CBSE board are the first public examinations that all students must attempt. The CBSE board exams assess the candidate's practical and theoretical knowledge. As a result, students must comprehend the principles, and connecting them to real-world applications will help them develop solid practical knowledge.
Our subject specialists develop the Class 10 NCERT Solutions to give a one-stop solution for all Maths queries. These Solutions for Class 10 NCERT provide an ideal platform for understanding all of the Maths ideas in the syllabus for students hoping to achieve in the CBSE Classes 10 Board Exam. The NCERT Solutions of solved examples and the exercise questions are explained with illustrated graphs and well-labelled diagrams that make learning effortless. It helps students create a strong conceptual point, which is crucial in the later phases of competing in competitive tests. The solutions to the NCERT-based questions for class 10 are easily accessible.
Solutions for Class 10 Maths NCERT include all the exercise problems from the NCERT Maths textbook. Our highly trained subject specialists have developed these Math answers to assist students in their test preparation. These answers will guide students in acquiring a higher grasp of the ideas taught in the Class 10 Maths curriculum. Students may assess their preparation and knowledge of statements by practicing NCERT Class 10 Maths textbook problems.
These assist students in comprehending or solving the sorts of problems that a paper setter asks in the first term examinations of CBSE Class 10 Maths. The subject matter experts make sure that the errors in the NCERT textbooks are resolved according to the NCERT rules and syllabus. The solutions to the NCERT-based questions for Grade 10 Maths are accessible through class 10 books. These solutions will assist students in acing their board examinations by preparing them ahead of time. Students may clarify all of their conceptual questions or doubts with the assistance of the notes of Maths NCERT Solutions for Class 10 of different chapters. Experts have created these NCERT Solutions based on the most recent update to the CBSE Syllabus to help students in Class 10 prepare well for their board examinations.
Students should complete Class 10 Maths NCERT Solutions after finishing the curriculum since it gives many problems from each unit to practice. Use these solutions to clarify any confusion, if anyone gets stuck when answering the issues, and supplementary references and study resources. All Math solutions are written unambiguously and prominently, considering the goal of textbooks. Students are urged to download and practice these solutions regularly to get a commendable rank in the Board exams. Students must comprehend all the processes outlined in the answers for successful preparation.
If you wish to strengthen your fundamental knowledge in several disciplines, the NCERT book is a fantastic place to start. It includes several diagrams, flowcharts, tables, and illustrations to supplement the various themes and concepts. It is a fantastic beginning point for people who wish to study a certain subject because it is designed to improve the fundamental understanding of pupils who read it. We think that after reading this, you will be grateful that we got your back, but this is not only for a subject.
The CBSE Class 10 math curriculum seeks to create learner knowledge and evaluation of basic concepts such as algebra, geometry, surface areas, volumes, statistics, and probability. The key to success in mathematics is practice. It is difficult to score well in this topic only by reading and memorizing the formulae; consequently, students are urged to practice them on a regular basis in order to obtain a good place in the board examinations. We provide class 10 Revision Notes for Mathematics so that students may quickly prepare all of the concepts included in the class 10 maths syllabus in a much better and more effective manner.
Maths Solutions for Class 10 include solutions to all of the questions and problems in the textbook. Real Numbers, Quadratic Equations, Triangles, Introduction to Trigonometry, Some Applications of Trigonometry, Area Related to Circles, Circles, Surface Areas and Volumes, and other topics are covered in Maths Solutions for Class 10. A team of subject specialists has developed Maths Solutions for Class 10, and the format follows the CBSE guidelines. It outlines each solution step by step so that students can comprehend it quickly, and marks are assigned to each step so that students may learn the answer writing skill from an exam standpoint.
We have supplied NCERT Class 10th Solutions to assist students in understanding the content, completing their assignments, and preparing for exams. With these answers, students will significantly improve their knowledge and problem-solving abilities. These solutions were developed under the supervision of professional educators and mentors while keeping the most recent NCERT curriculum in mind to provide you with up-to-date material. The questions and solutions are explained step-by-step in depth so that you can better comprehend them. Each subject presents solutions with brief details to give you the necessary context.

How can one understand the key ideas taught in the NCERT Solutions for Class 10 Maths?
Ans. Students who want to do well in their Class 10 examinations should get the NCERT Solutions for class 10 maths books. A group of teachers with extensive knowledge in the particular area curates the solutions with great care. Every minute topic is discussed engagingly to make studying easy for the pupils. The step-by-step answers are created using the marks weightage provided by the CBSE in mind.
Will the NCERT Solutions for Class 10 Maths make it easier for me to tackle the problems?
Ans. The Class 10 test is a watershed moment in the lives of learners. Mathematics is a topic that mainly consists of numerical, and comprehending ideas helps to obtain higher grades. Students should first comprehend the academic year's syllabus and then master the topics based on it for better performance. Students' logical thinking and analytical abilities will develop as they solve textbook problems using the answers PDF.
How can I obtain the NCERT Solutions for Class 10 Maths PDF?
Ans. Class 10 books provide students with NCERT Solutions for Class 10 Maths PDF. Subject matter experts prepare the solutions with the students' learning capacity in mind. The primary goal of developing solutions is to assist students in learning complicated ideas without trouble. Students can also cross-check their answers while working through textbook problems to obtain a sense of other approaches to resolving topics quickly.
Are the NCERT Solutions for 10th Grade Maths beneficial to CBSE board students?
Ans. Some of the specific applications of the NCERT Maths Solutions for Class 10 -
How can I acquire a sense of the key concepts in the NCERT Solutions for Class 10 Maths?
Ans. Students should download and read the CBSE curriculum before the start of each academic year to have a thorough grasp of the subjects that will be assessed. Students must tackle NCERT Textbook issues by selecting the appropriate study resource that meets their needs. Students' problem-solving abilities improve when they practice the problems on a regular basis using the NCERT Solutions for Class 10 Maths.
Is it necessary to use the NCERT Solutions for Class 10 Maths?
Ans. NCERT Solutions for Class 10 Maths are designed in such a way that students may quickly comprehend the concepts and solve their difficulties. The answers include detailed explanations to help students understand the subject. Students can get PDF solutions and utilize them to strengthen their conceptual understanding.
Are the NCERT Solutions for Class 10 Maths the finest resource for CBSE students?
Ans. Students should choose the best study material for their needs from the many options available on the market. Class 10 books NCERT Solutions for Class 10 Maths are widely regarded as the finest reference tool for CBSE students. The solutions are given in chapter and practice forms, which students may download and utilize. Students can view the PDF links without regard to time limits.
Why do students require NCERT Solutions for Class 10 study material to qualify for the board exam?
Ans. Class 10 is an important time in a student's life since the grades they receive determine their future profession. It might be challenging to achieve good results in board examinations without adequate study materials. NCERT Solutions for Class 10 in a subject-by-subject manner. Students who are having problems answering textbook questions can use these solutions to ace the board test easily.
Explain the significance of class 10 books NCERT Solutions for Class 10.
Ans. The significance of class 10 books NCERT Solutions for Class 10 is as follows:
How can one obtain free NCERT Solutions for Class 10 PDFs from OSWAAL?
Ans. As class 10 is a critical phase in students’ life, students should choose the appropriate study material that meets their demands. Keeping this in mind, the team of subject matter experts curate solutions that are clear and easy to grasp. The solutions include step-by-step explanations to enable students of all IQ levels to understand the ideas. The PDFs of the answers may be downloaded by visiting the our website. By inputting the necessary information, students will have access to both online and offline study resources for a particular subject.
Will the board exam questions be drawn from NCERT Solutions for Class 10 Maths?
Ans. The NCERT Solutions for Class 10 Maths provide the most questions in the board exam. Students can refer to the solutions offered by the professors at class 10 while answering textbook problems to gain a better knowledge of the subject. The answers are designed so that students may easily comprehend complicated concepts. Students can utilize online and offline solutions with no time limits.
How many exercises are there in the Grade 10th Maths Chapter 12?
Ans. There are three exercises are present in the 10th Grade Maths Chapter 12, i.e., Areas Related to Circles.
How many problems are present in each NCERT Exemplar Solutions for Class 10 Maths Chapter 12 exercise?
Ans. Three problems are included in Chapter 12 of the NCERT Solutions for Class 10 Maths. Exercise 12.1 consists of five questions, whereas Exercise 12.2 consists of 14 questions. 12.3 comprises 16 questions. Every problem is addressed with the utmost attention to give students accurate solutions following CBSE norms.
Explain the circumference of a circle in Chapter 12 of NCERT Exemplar Solutions for Class 10 Maths?
Ans. A circle's perimeter is the linear distance travelled around the circle. The perimeter of a circle is known by a unique name, Circumference. The circumference multiplied by the diameter is given by the formula 2πr.
Where can I get online NCERT Exemplar Solutions for Class 10 Maths Chapter 12?
Ans. Yes, the NCERT Exemplar Solutions for Class 10 Maths Chapter 12 are available on our website. Subject specialists evaluate the solutions to all problems to give students the most significant reference material. You can download chapter-by-chapter or exercise-by-exercise answers to understand better the problem-solving approaches used while solving textbook questions
Which chapter in class 10 math is the most difficult?
Ans. The most challenging chapter is trigonometry.
In Class 10, how many hours should I study?
Ans. A student should study between 7 and 10 hours every day. It is probable that if you dedicate more time, you may become weary. As a result, the maximum amount of time you should commit to your studies is 7 – 10 hours.